理由
“a robust L1 loss that is less sensitive to outliers than the L2 loss used in R-CNN and SPPnet.” 意思是L1比L2对其在异常点不敏感,两方面来说明: 1、当预测框与 ground truth 差别过大时,梯度值不至于过大; 2、当预测框与 ground truth 差别很小时,梯度值足够小。

观察 (4),当增大时损失对的导数也增大。这就导致训练初期,预测值与 groud truth 差异过于大时,损失函数对预测值的梯度十分大,训练不稳定。 根据方程 (5), 对的导数为常数。这就导致训练后期,预测值与 ground truth 差异很小时,损失对预测值的导数的绝对值仍然为 1,而 learning rate 如果不变,损失函数将在稳定值附近波动,难以继续收敛以达到更高精度。 最后观察 (6),在较小时,对的梯度也会变小,而在很大时,对的梯度的绝对值达到上限 1,也不会太大以至于破坏网络参数。完美地避开了和损失的缺陷。
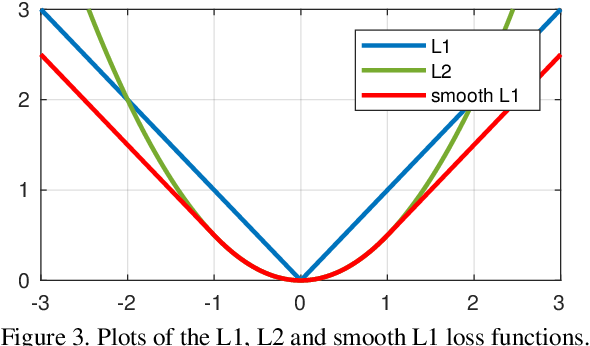
结论
| 1、当if | x | > 1时的情况,smooth L1 loss让loss对于离群点更加鲁棒,相比于L2损失函数,其对离群点、异常值(outlier)不敏感,可控制梯度的量级使训练时不容易跑飞, 避免梯度爆炸。 |
| 2、当if | x | < 1时的情况,Smooth L1 Loss结合了L2 Loss收敛更快,且在0点有导数,便于收敛的好处。 |